Capacitors Introduction and Modelling

What are capacitors?

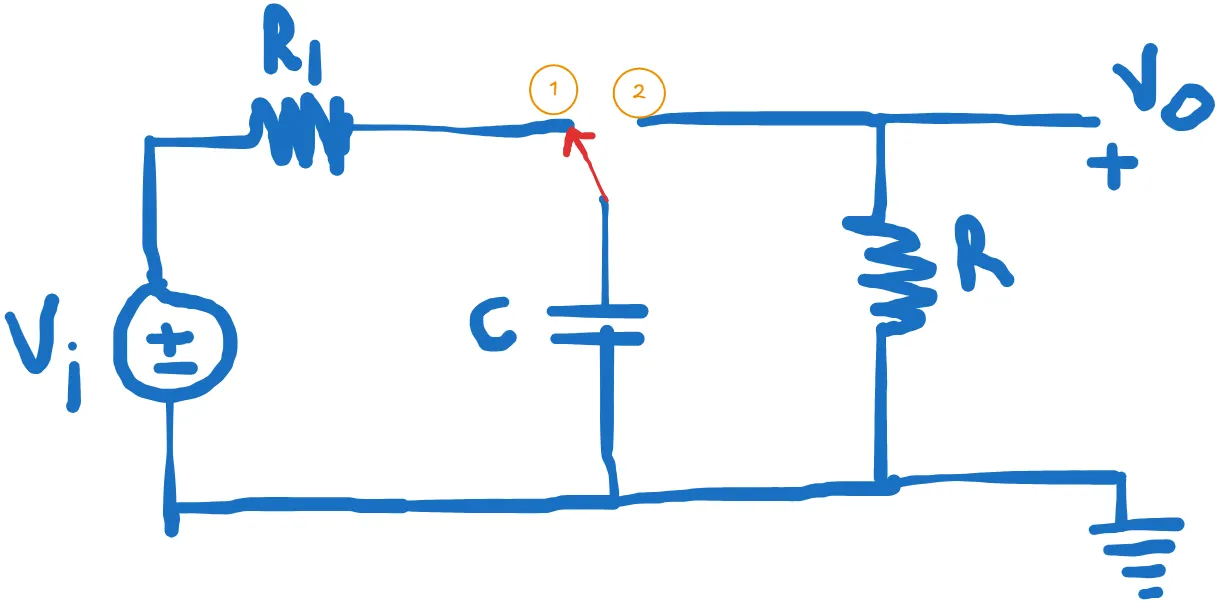
base circuit image

Figure 1: Base Circuit Image

A capacitor is defined as a passive component which is used for storing electrical energy. A capacitor is made of two conductors that are separated by the dielectric material. These dielectric materials are in the form of plates which can accumulate charges.
One plate is for a positive charge while the other is for a negative charge.
Capacitance is the effect of the capacitor. Capacitance is defined as the ratio of electric charge Q to the voltage V and it is expressed as

C = \frac{q}{v}

Where,

Q is the electric charge measured in coulombs
C is the capacitance measured in farad
V is the voltage across the plates measured in volts

Capacitors Modelling

Starting with the Capacitor modelling equation:

I = C \cdot \frac{dv}{dt}

\frac{I}{C} * dt = dv

And now assuming that the circuit is operating for 0 to time t we get:

v(t) = v(0) + \frac{1}{C} * \int_0^t I \, * dt

This formula states that the current I measured in amps, flowing in a capacitor is equal to the capacitance C measured in farads times the rate change of voltage measured in volts per second. Figure above shows the schematic symbols used for capacitors and the current direction convention (+ to – is positive).

Notice that some capacitors are polarized, others are bipolar or monolithic. Typically, polarized capacitors have much larger values that monolithic or bipolar types.

Capacitor Charging and Discharging states

RC Discharging Analysis

The current going out of capacitor in diagram 2 above is :

\begin{align*} V &= IR \nonumber \\ I &= \frac{V}{R} \nonumber \\ \end{align*}

$I$ is negative below as current flows from capacitor into the opposite side as in the second image above

\begin{align*} I &= - C \cdot \frac{dv}{dt} \tag{1} \\ \end{align*}

Hence, this can be resolved as:

\begin{align*} &\frac{V}{R} = - C \cdot \frac{dv}{dt} \\ \\ &\boxed{\frac{dv}{dt} = -\frac{1}{RC}.V} \tag{1.1} \end{align*}

This is the differential function, this means that the slope of the function equals some constant times the function.

The equation

V = Ae^{-t/\tau}

Taking the derivative of this function at time $t_{0}$ will result in:

\begin{align*} & V_{0} = A.e^{-0/\tau} \tag{2} \\ \\ & \text{therefore,} \\ \\ & V_{0} = A \end{align*}

Substituting $V_{0} = A$ we get following equation:

\begin{align*} & V = V_{0}.e^{-t/\tau} \tag{2.1} \\ \\ & \text{on differentiating on both sides we get,} \\ \\ & \frac{dv}{dt} = V_{0}.\left( -\frac{1}{\tau} \right).e^{-t/\tau} \tag{2.1.1} \end{align*}

considering $(eq. 1.1)$ we get:

\begin{align*} V_{0}.\left( -\frac{1}{\tau} \right).e^{-t/\tau} = -\frac{1}{RC}.V \\ \\ \text{which would reduce to} \\ \\ V_{0}.\left( -\frac{1}{\tau} \right).e^{-t/\tau} = -\frac{1}{RC}.V_{0}.e^{-t/\tau} \\ \\ \text{eliminating commons on both end,} \\ \\ \left( -\frac{1}{\tau} \right) = -\frac{1}{RC} \\ \\ \text{would yield us } \\ \\ \boxed{\tau = {RC}} \tag{3} \\ \\ \end{align*}

And the final equation that we get for discharging of capacitor after substituting above equation inside $eq.2.1$ is:

\boxed{V_{t} = V_{0}.e^{-t/RC}} \tag{3.1}

where RC is the time constant.

The equations that we solved above depicts the following chart:

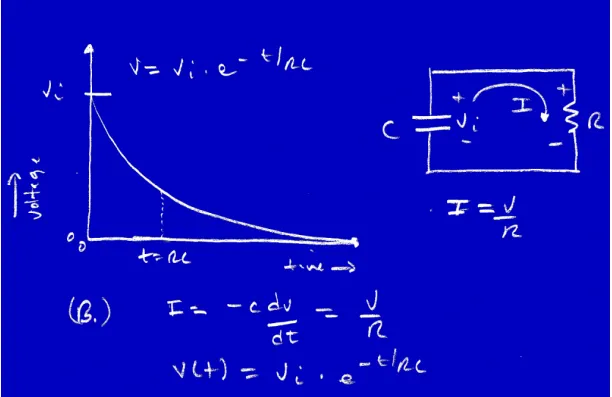capacitor discharging This is how the graph looks when capacitor is discharging.

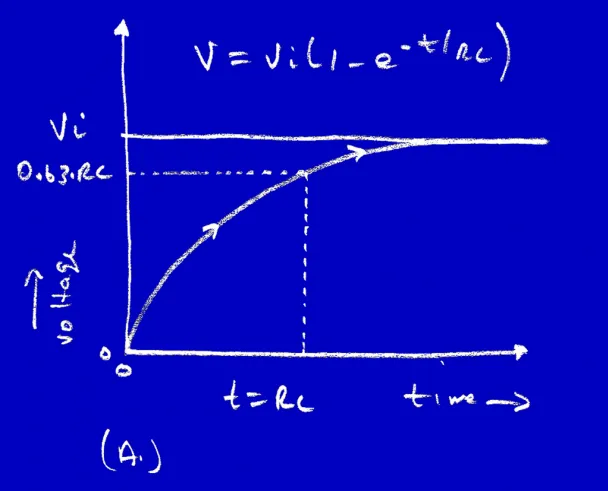
RC Charging Analysis

Considering that the voltage is driving out of batter in diagram 1 above, we can assume that the capacitor is at 0 charge on it at the moment before closure, we can write a simple equation that describes the circuit.

The circuit is driven with a voltage source Vi, this creates a current thru resistor R that charges C, the current Ic must be the same through the resistor as well as the capacitor, so we can write:

I_{c} = C \cdot \frac{dv}{dt}

Deriving, $I_{c}$ also from the $I=\frac{v}{r}$ formula we can write:

I_{c} = \frac{(V_{i}-V)}{R}

Here we do $V_{i}-V$ because as per the diagram, we consider source voltage - voltage across capacitor. So, our modeling equation becomes:

C \cdot \frac{dv}{dt} = \frac{(V_{i}-V)}{R}

This is first order differential and based on the equations inside RC discharging at $eq. 2.1$ :

\frac{dv}{dt} = \left( \frac{-t}{rc} \right)*Ae^{-t/RC}

plugging V into the modeling equation along with the derivative of V with respect to $t$ we get:

\boxed{V = V_{i} + Ae^{-t/RC}} \tag{4}

Right at the moment of closure of the switch that is t=0-, (0- means an infinitesimal amount of time before 0, and similarly 0+ means an infinitesimal amount of time after 0) the capacitor had 0 charge on it, therefore, 0V. Hence, we can write this

\begin{align*} & 0V = Vi + A*e^{-0/r*c} = Vi + A*e^{-0/r*c} = Vi + A*e^0 = Vi + A*1 \\ \\ & 0V = Vi + A, A = -Vi \\ \\ \end{align*}

Hence, substituting the value of A as $V_{i}$ in $eq. 4$ we get:

\begin{align*} & V = Vi - Vi*e^{-t/rc} \\ \\ & \boxed{V = Vi(1-e^{-t/rc})} \tag{4.1} \\ \end{align*}

RC Charging results in table:

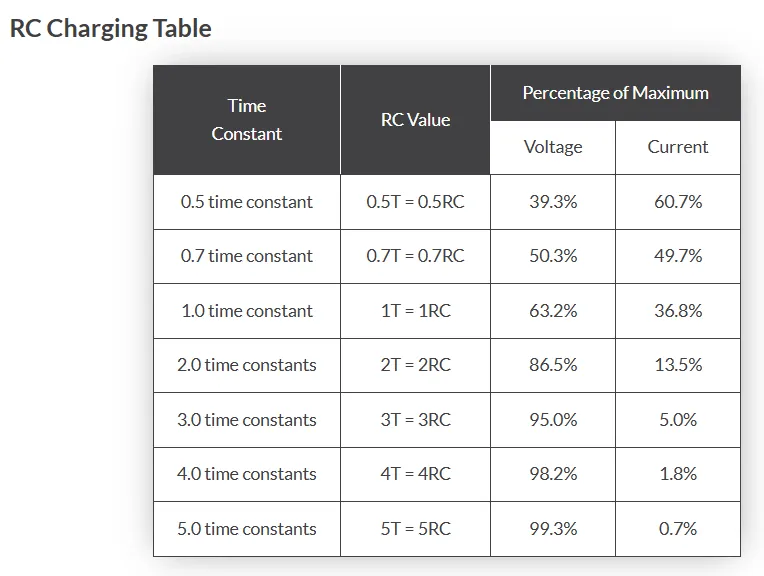RC Charging table image from electronics-tutorials.ws

From the table above we can substitute the values inside the final equations and can prove that at 5RC times our capacitor will be almost 99% fully charged:

Assuming, we’re using 9v battery to energize the circuit shown in diagram 1 of capacitor charging circuit, then substituting 9v and 5rc times in the formula $V = Vi(1-e^{-t/rc})$ we get,